«Ainsi procède-t-on le plus souvent dans les sciences démonstratives, et cela parce que, si la conclusion est vraie, on retrouve aisément, en employant la méthode résolutive, quelque proposition déjà démontrée où on remonte à quelque principe évident; si au contraire, la conclusion est fausse, on procède indéfiniment sans jamais rencontrer aucune vérité connue, ou même on aboutit à une absurdité manifeste.»

Ici, Galilée fait référence aux sciences démonstratives
(mathématiques, mais également théologie),
avec leurs méthodes logiques: on pose des hypothèses
concernant une question physique, métaphysique ou religieuse.
On applique ensuite les règles de la logique déductive.
On parvient à la vérité des hypothèses.
Cela, sans vérification expérimentale, avec les lois de la simple raison logique.
Inversement, le raisonnement peut parvenir à une conclusion fausse
par rapport aux principes évidents :
les hypothèses sont alors fausses

Mais est-ce comme cela que doivent fonctionner les sciences de la nature?
Salviati explique alors que même dans les mathématiques,
on vérifie expérimentalement ses hypothèses...

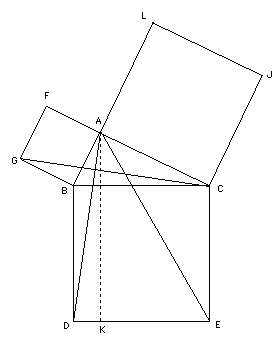«Ne doutez pas que Pythagore, longtemps avant d'avoir trouvé la démonstration pour laquelle il fit l'hécatombe (NDE: il s'agit du théorème de Pythagore : ci-joint, démonstration par Euclide), s'était assuré que le carré du côté opposé à l'angle droit était égal à la somme des carrés des deux autres côtés; aussi bien la certitude de la conclusion n'est-elle pas d'un médiocre secours pour la découverte de la preuve, toujours bien entendu, dans les sciences démonstratives. Quel que fût au surplus le procédé d'Aristote, qu'il ait fait passer l'a priori du raisonnement avant l'a posteriori du sensible, ou inversement, il n'en reste pas moins que (comme on l'a souvent rappelé) il met l'expérience des sens au-dessus de tout discours. Enfin, quant aux raisonnements a priori, nous avons déjà examiné quelle est leur force.»

Galilée règle ses comptes au passage avec les théologiens
et philosophes scolastiques qui ergotaient à longueur de journée
à partir de raisonnements a priori.

-

Retour page accueil Galilée